In Elucidations Episode 51, Groenendijk and Roelofsen sketch out some of the merits of the inquisitive semantics approach to questions in contrast to the ‘classical’ semantic approach. One stark area of contrast is with respect to conditional questions—questions like: “If Matt drinks coffee, does Phil drink coffee?” Groenedijk and Roelofsen observe that the classic semantic approach to questions cannot easily accommodate these conditional questions. In this post, I’d like to flesh out this observation just a bit more.
The ‘classical’ semantic approach that we are working with takes the proposition the primary unit of analysis. That is, we start by laying out the truth conditions of propositions, and then build the rest of our semantic framework around this bedrock. Remember that ‘proposition’ is jargon for the content of a sentence. For example, we say that the proposition expressed by the sentence “Julie got an A on her philosophy paper” is that Julie got an A on her paper; we say that the sentence is true when Julie in fact gets an A on her paper. Our classical semantics picture fleshes this out a bit more by introducing the idea of ‘possible worlds:’ formally entities meant to represent logically coherent states of affairs (i.e.: they contain no logical contradictions). We then say that a proposition is the set of worlds in which the sentence is true—the set of possible words in which Julie in fact got an A on her paper. For more on possible world semantics, see Matt’s post here: Possible Worlds Semantics.
Now, it is quite clear that questions do not have truth conditions like declarative sentences (assertions) do: while we can say that “Julie got an A on her philosophy paper” is either true or false (depending on how the actual world turns out), we can’t say this about a question like “Does Matt drink coffee?” (If you asked me this question, and I responded ‘false,’ you’d probably give me a strange look, or assume that I was giving a more pretentious rendering of the ordinary answer, “no.”) Instead, the classical semantic view will lay out ‘answer conditions:’ a set of answers to the question that exhausts logical space (all the possible sensible answers to the question), and are mutually exclusive to one another (i.e.: the answers don’t have any ‘overlapping’ possible worlds).
Let’s take an example to sketch this out. Assume that all of logical space (everything that is logically possible) can be decomposed into the following four possible worlds:
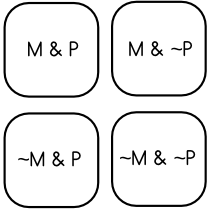
(1)
where ‘M’ stands for “Matt drinks coffee,” ‘P’ stands for “Phil drinks coffee,” ‘~’ for “not” (so ‘~P’ means “Phil does not drink coffee”) and ‘&’ for “and” (so ‘M & ~P’ stands for “Matt drinks coffee and Phil does not drink coffee”).
How would the classical semantic approach treat the question: ‘Does Matt drink coffee?’ The first thing we would do is note that there are two sensible answers to this question: ‘yes,’ and ‘no’ (we’ll leave aside the uncertainty associated with ‘maybe’). Each of these answers, on the classical semantic approach, should capture a set of possible worlds, together exhaust all of logical space, and exhaust logically space without overlapping each other.
Which possible worlds does the answer ‘yes’ capture with respect to the question ‘Does Matt drink coffee?’ Those in which Matt drinks coffee; that is, those worlds in our possibility space above that contain ‘M.’
How about for ‘no?’ Those worlds in which Matt does not drink coffee; that is, those worlds in our possibility space above that contain ‘~M.’
So we end up with the following semantic picture of ‘Does Matt drink coffee:’
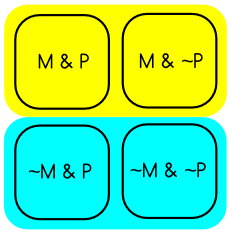
(2)
where the ‘yes’ worlds are in yellow, and the ‘no’ worlds are in blue. Note that every possible world falls under one, and only one, of the possible answers to the question.
All well and good so far, but what about conditional questions? Take, for example, ‘If Matt drinks coffee, does Phil drink coffee?’ Just like the last question, we’re inclined to say that there are two possible answers to this conditional question: ‘yes’ and ‘no.’ These answers correspond to the following conditionals:
Yes: If Matt drinks coffee, then Phil drinks coffee.
No: If Matt drinks coffee, then Phil does not drink coffee.
(Note that the conditional question we are treating is very different than the question: ‘Is it true that if Matt drinks coffee, then Phil drinks coffee?’ That question, even though it contains a conditional, has two non-overlapping answers, just like ‘Does Matt drink coffee?’)
When would we be inclined to answer ‘yes’ to the conditional question? When the conditional ‘If Matt drinks coffee, then Phil drinks coffee’ is true. And this conditional is true either when the antecedent (‘Matt drinks coffee’) is false, or when the consequent (‘Phil drinks coffee’) is true. (Here we are assuming that the conditional question is expressing a ‘material conditional,’ which is true in all cases except where the antecedent is true and the consequent false; where Matt does drink coffee, but Phil does not.) So the answer ‘yes’ captures these three possible worlds in our framework above:
- M&P
- ~M & P
- ~M & ~P
(Not ‘M & ~P,’ because this is a case in which the antecedent of the ‘yes’ conditional is true and the consequent false.)
Let’s do this again for the ‘no’ answer. When would I answer ‘no’ to the question: ‘If Matt drinks coffee, does Phil drink coffee?’ When it is the case that if Matt drinks coffee, then Phil does not drink coffee. When is this conditional true? When either Matt does not drink coffee, or when Phil does not drink coffee (i.e.: when the antecedent is false or the consequent is true). So the answer ‘no’ captures these three possible worlds in our framework above:
- M & ~P
- ~M & P
- ~M & ~P
(Not ‘M & P,’ because this is a case in which the antecedent of the ‘no’ conditional is true and the consequent false.)
Remember that on the classical semantic approach, the answers to the question should exhaust logical space in a mutually exclusive way (i.e.: no overlap). Is this what we get if we combine our ‘yes’ and ‘no’ answers to the conditional question?
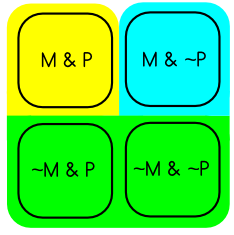
(3)
No! We get some overlap (marked by the green highlight; remember that ‘yes’ is yellow and ‘no’ is blue). While we’ve exhausted all of logical space, our answers do not carve it up in a mutually exclusive way. So the classical semantic approach to questions cannot satisfy one of its own requirements (that answers to a question carve up logical space in a mutually exclusive way).
What’s going on here? An astute reader might that the ‘problem worlds’ (where the overlapping occurs) are those in which Matt does not drink coffee—those in which the antecedent of both the ‘yes’ and ‘no’ conditionals corresponding to the conditional question is false. One temptation, then, is to resolve the failure by getting rid of these ‘problem worlds.’ That is, we might think that when one asks “If Matt drinks coffee, does Phil drink coffee?” what we are really asking is ‘Assuming Matt drinks coffee, does Phil drink coffee?’ (to get at this intuition, put the emphasis on ‘if’ in the original question). If what we really mean is ‘assuming Matt drinks coffee, does Phil drink coffee,’ what we are doing is ruling out those worlds in which Matt does not drink coffee—we are shrinking the logical space under consideration. In that case, we would end up with:
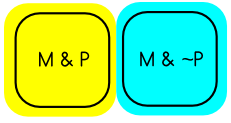
(4)
Yellow for ‘yes, Phil does drink coffee’ (assuming Matt does), and blue for ‘no, Phil doesn’t drink coffee’ (assuming Matt does).
The problem with this sort of approach is that, while perhaps some conditional questions can be interpreted as really meaning ‘assuming X, then?’, not all can. That is, at least in some cases of conditional questions, we are really asking about the material conditionals ‘If X, then Y’ and ‘If X, then not Y.’ And when we do ask conditional questions about material conditions, we do in fact run into this problem of overlapping answers. And that fact is what entails the inadequacy of the classical semantic approach to questions (because it fails for at least some conditional questions—as well as some disjunctive questions), and thus opens up space for the inquisitive semantics approach Groenendijk and Roelofsen are pioneering.
(Much thanks to Matt for some exceptionally helpful discussion on this topic (and with the diagrams)!)
Phil Yaure
Leave a Reply