Bayes’ Theorem

In the first part of this post, we talked about the motivations behind the epistemic interpretation of probability. Now, let’s take a look at one of the core mathematical theorems employed by those who subscribe to such an interpretation: Bayes’ Theorem (which is mentioned by Fitleson in Ep. 31).

Before introducing Bayes’ Theorem, it is important to get clear on one last concept: conditional probability. The basic idea behind conditional probabilities is that we offer the probability that some event occurs, given that something else is true. It’s helpful to think about this once again in a gambling analogy. Let’s say that we want to bet on whether the Philadelphia Phillies will win the World Series next year. I might only wish to make a bet on this if one of their star players (say, Ryan Howard) is not injured this year. So we might make bets conditional on Ryan Howard not becoming injured—if Howard is injured, the bet is simply off. Referencing another of our blog posts, we say that conditional probabilities restrict the set of possible worlds we are considering (say, those possible worlds in which Ryan Howard is not injured for the 2013 season), and compute the probabilities from this restricted set of possible worlds.

Now we can introduce Bayes’ Theorem. The theorem takes the following form:

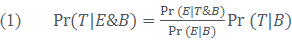
(There’s a bit more mathematical machinery behind even this, but we won’t worry about it.) How do we read this equation? Well, let’s start with one of the smaller parts:

We can read this as: the probability of T given B. That is, we’re considering the conditional probability of T given that B is true. The whole thing, (2) will spit out some value between 0 and 1 (inclusive). We can read the rest of the parts in the same way, taking ‘T & B’ or ‘E & B’ as expressing T and B or E and B.

Now let’s break the equation down into its other parts:

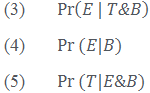
So each Pr(…) on the right spits out some value between 0 and 1 (inclusive) and we multiply (2) by the ratio (3) over (4) and to give us some other value, represented by (5). Now let’s make things a bit more concrete. We can take ‘T’ to stand for some theory or hypothesis that we are interested in evaluating our degree of belief in. ‘B’ can stand for all of the background information that we presuppose (if T is some hypothesis in physics, B can stand for everything we already know is true about physics). ‘E’ can stand for some new event or evidence (say, some new experiment in a physics lab).

We can thus read each part of Bayes’ Theorem in the following way:

(2): We call this this the ‘prior’ probability. This is the probability that T, our hypothesis, is true simply in virtue of the B, the background information we’ve taken for granted (say, our existing knowledge of physics).

(3): We call this the ‘likelihood.’ This is the probability that E, some new event—say the result of some physics experiment we’ve just done—is true assuming that our hypothesis T and background information B are true.

(4): We call this the ‘expectedness.’ This is the probability that E is true just given our background information B, regardless of whether our hypothesis T is true.

(5): We call this the ‘posterior’ probability. This is the probability that our hypothesis T is true, given that our experiment E and background information are true.

With Bayes’ Theorem, we can compute the posterior probability (that T is true given E and B) by multiplying our prior probability (that T is true just given B) by the ratio of the likelihood and expectedness. On an epistemic interpretation of probability, this amounts to a model for changes in our degree of belief in our hypothesis T given some new evidence E.

Let’s conclude with a simple example, borrowed from Fitleson’s episode. Take a standard deck of cards, where we want to know the probability that the ace of spades will be drawn. We can start by computing our prior probability—that is, the probability that the ace of spades will be drawn given our background information about a standard deck of cards. In this case, (2) = 1/52, as there are 52 cards in the deck, and one of them is the ace of spades.

Now let’s say that we are told that the card drawn is of a black suit. What should be our degree of belief that the card drawn is the ace of spades? We can use Bayes’ Theorem to compute this. We already have our prior probability, 1/52, so we just need to compute the likelihood and expectedness.

Likelihood: Remember that the likelihood is (3). Here, this means the probability that card drawn is black (E), given our knowledge of a standard deck (B) and that the card drawn is in fact the ace of spades (our hypothesis, T). Well, since the ace of spades is black, and we’re assuming that T is true in order to calculate the likelihood, the likelihood is 1.

Expectedness: Remember that the expectedness is (4). Here, this means the probability that the card drawn is black (E), just given our knowledge of a standard deck of cards (B). Since half the cards in the deck are black, this probability is 1/2.

Now we can combine these three computations to get our posterior probability, (5), the probability that the ace of spades is drawn (T), given that the card drawn is black (E) and our knowledge of a standard deck of cards (B):

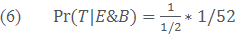
Or 1/26. Bayes’ Theorem models the behavior of a rational agent in these circumstances, who comes to know that the card drawn is black, and adjusts her degree of belief that the card drawn is the ace of spades accordingly. This model can be generalized to a whole variety of circumstances—in particular, Bayesians will often apply Bayes’ Theorem in the philosophy of science to model changes in scientists’ degree of belief in some theory given the introduction of new evidence. Many interesting results come out of this application, which we’ll have to save for a later post. Hopefully, though, we’ve given you an idea of (some of) the motivations for an epistemic interpretation of probability, and the mathematical machinery that such an interpretation can employ.

Phil Yaure